Principles of mapping

Maps are staples of visual storytelling: You often want to communicate the “where” for the action being described. Unlike some chart types, which may require some explanation to the uninitiated, maps need no introduction — we are all familiar with using them to navigate. Indeed, thanks to the smartphone revolution, many of us now carry sophisticated interactive mapping apps everywhere we go.

Maps can also be used to visualize data, which will be our main focus in this workshop as we process geodata and learn how to display it on both static and online maps. Before we jump into making maps, we will cover some basic principles of mapping, and good practice in mapmaking.

The basics: latitude and longitude

Consider the following concepts in relation to this image:

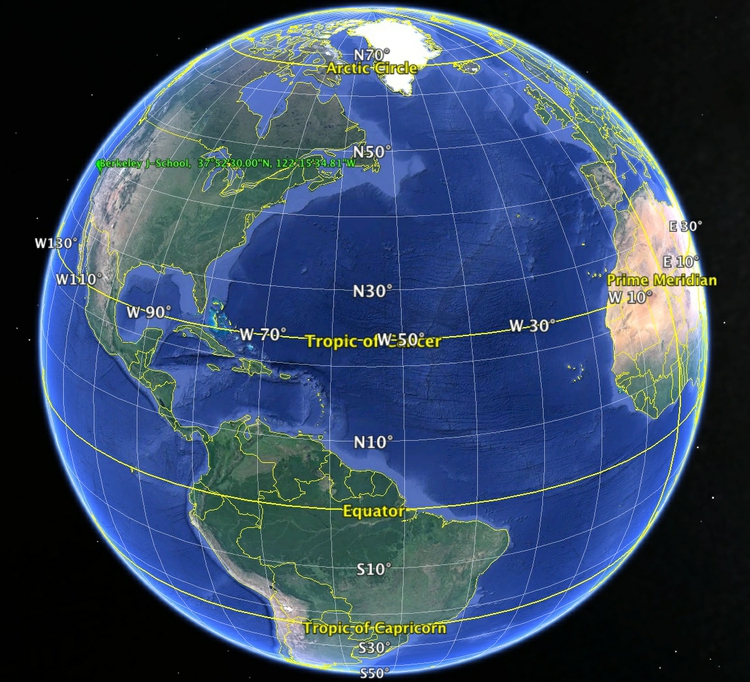
(Source: Google Earth)

When plotting points on a map, you will usually need to know their latitude and longitude. Latitude and longitude is a geographic coordinate system that enables every location on the Earth’s surface to be defined by two numbers. Latitudes are angular distances, given in degrees from 0 to 90, which define how far North or South a point is from the Equator. Longitudes are angular distances, given in degrees from 0 to 180, which define how far East or West a point is from a line running from the North to the South Pole through the Royal Observatory in Greenwich, London. Lines of equal latitude are known as parallels, while lines of equal longitude are called meridians.

Degrees of latitude or longitude can be subdivided into minutes and seconds (sometimes called the DMS system), or can be given as decimals. There are 60 minutes in a degree, and 60 seconds in a minute; the symbols for degrees, minutes and seconds are: °, ' and ". In decimal format, points North of the Equator are given as positive values, while those South of the Equator are negative. Similarly, for longitude, points to the East of the Prime Meridian that runs through Greenwich are positive, while those to the West are negative.

To understand how this works, consider the location of the UC Berkeley Graduate School of Journalism. Its latitude and longitude coordinates are 37.8749998 and -122.2596684, which can also be written as 37° 52' 30.0" N , 122° 15' 34.8" W. If you were to draw a line from the center of the Earth to the J-School, and then draw another to the Equator at the same longitude, the angle between them would be 37.8749998 degrees. If you were to take a slice of the Earth at this latitude, parallel to the equator, and draw two lines from the center of this slice, one to the Prime Meridian, the other to the J-School, the angle between them would be -122.2596684 degrees.

(Various online services support conversion from DMS to digital latitudes and longitudes, and vice versa — the two links given are free to use, and will process many thousands of records at a time.)

There are 360 degrees in a full circle, which explains why longitude goes from 0 to 180 degrees both East and West. Similarly, moving from the North to the South Pole means travelling half way round the Earth’s circumference, which is why latitude goes from 0 to 90 degrees both North and South.

Two points separated by one degree of latitude, lying at the same longitude, will always be separated by about 69 miles, because meridians are always the same size, representing half the circumference of the Earth. However, parallels decrease in size as we move nearer to the poles. At the Equator, one degree of longitude again corresponds to a linear distance across the Earth’s surface of about 69 miles. But at 45 degrees latitude North or South, you would need to travel just 49 miles to cover one degree of longitude.

Map projections

Because the Earth is roughly spherical, any map other than a globe is a distortion of reality. Just as you can’t peel an orange and arrange the skin as a perfect rectangle, circle, or ellipse, it is impossible to plot the Earth’s surface in two dimensions and accurately represent distances, areas, shapes and directions.

Maps can be made simply by plotting latitude on the X axis and longitude on the Y axis on the same scale, sometimes called an Equirectangular projection:

(Source: Wikimedia Commons)

Most maps are drawn according to a more sophisticated projection system, however. There are many different systems, each of which has advantages and drawbacks. Some projections are optimized to minimize the distortion of area; others aim to preserve shape or distance; yet others keep directions constant.

Google and most other online maps use a Mercator projection, which was originally designed for navigation at sea. The main strength of the Mercator projection is that it preserves direction, so that any straight line drawn on the map is a line of constant compass bearing. Parallels are all horizontal and meridians vertical. This preservation of direction is also a good choice for zoomable maps used primarily for local orientation. The big drawback of this projection is that it distorts area and shape, especially at high latitudes, which makes it a poor choice for representing the entire world. Notice how the distances between parallels increase with latitude:

(Source: Wikimedia Commons)

When mapping the continental United States, particularly when coloring or shading different areas according to the values of data, it is common to use the Albers Equal Area Conic projection, as seen in this map of siesmic risk:

(Source: Peter Aldhous, from U.S. Geological Survey data)

As the name suggests, this projection minimizes distortions of area. It does not preserve direction: Notice that the border with Canada, which runs along a parallel at a latitude of 45 degrees N, is a curve, rather that a straight line.

The Albers Equal Area Conic projection is rarely used to show the entire Earth, for obvious reasons when you see the projection in global view:

(Source: Wikimedia Commons)

To minimize the distortion of area on a global map, a better choice is the Mollweide projection:

(Source: Wikimedia Commons)

The Mollweide projection is also often used for maps of the entire sky (which can be thought of as the inside of a sphere). I used it here to compare the resolution of maps of the cosmic microwave background radiation, which reveal ripples in space-time that are the remnants of conditions in the early Universe, with views of the Earth:

(Source: New Scientist)

The Mollweide projection’s main disadvantage is the distortion of shape at high latitudes and longitudes — look, for example, at Alaska on the above Mollweide maps.

Under certain circumstances, preserving distance may by the most important goal. Here, an Azimuthal Equidistant Projection is the best approach:

(Source: Wikimedia Commons)

This projection would be the best choice, for example, when making a map centered on North Korea to illustrate the locations that might lie within the range of the nation’s ballistic missiles.

(Note from this example that that projections can be centered on any point on the Earth — they do not have to be centered on the intersection between the Equator and the Prime Meridian, which is the most common view for a global map.)

Distortions of shape, area, distance and direction are not so noticeable when mapping small areas, but become obvious and potentially distracting when representing the entire globe. Under these circumstances, mapmakers often adopt a compromise projection in which distance, area, shape, and direction are all distorted, but to a minimal extent. An example is the Robinson projection:

(Source: Wikimedia Commons)

In addition to a projection, a map also has a datum, which refers to a mathematical model accounting for the shape of the Earth — which is not a perfect sphere. Under most circumstances, however, you will not need to worry about this.

Putting data onto maps

Visualization: encoding data using visual cues

Whenever we put data on a map, we are encoding data using visual cues — using variation in size, shape, color or other attributes to represent values in the data. There are various ways of doing this, as this primer illustrates:

These visual cues are not created equal, however. In the mid-1980s, statisticians William Cleveland and Robert McGill ran some experiments with human volunteers, measuring how accurately they were able to perceive the quantitative information encoded by different cues. This is what they found:

This perceptual hierarchy of visual cues is important, and presents some challenges when making maps. When making comparisons between numerical values, you should aim to use cues nearer the top of the scale wherever possible. But you can’t easily plot length on an aligned scale on a map.

Cues near the bottom of the heirarchy, meanwhile, can still be useful for making more generic comparisons. In particular, color hue can a good way of encoding categorical data — for instance denoting whether or not U.S. states use the death penalty.

Scaled circles vs. choropleth maps

Data can be put onto maps in various ways. When numerical values are plotted to points, one common approach is to use circles centered on each point, sized according to the data values. Here is an example of this approach, showing historical earthquakes in North America:

(Source: Peter Aldhous, from U.S. Geological Survey data)

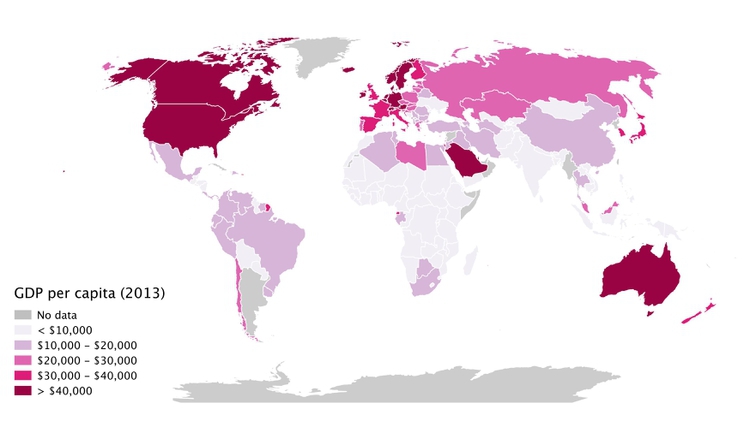
When plotting data to geographical areas, the most common approach is to fill the areas with color according to the data values, like this map of GDP per capita for the world’s nations in 2013:

(Source: Peter Aldhous, from World Bank data)

These are known as choropleth maps, and they have an important drawback: Our eyes are drawn to expanses of color, which means that large geographic areas will attract greater attention, whether or not these are actually more important for the story you are trying to tell from the data.

For this reason, scaled circles located to the center of geographic areas may sometimes be a better option. Here, for example, is the map of GDP per capita redrawn using this method:

(Source: Peter Aldhous, from World Bank data)

Notice that the two largest circles, for the territories with the highest GDP per capita, represent Qatar, on the Arabian Peninsula, and Macao, on the coast of southern China. Qatar was barely visible on the choropleth map, and Macao was too small to be noticed.

(Note, because the area = π * radius^2, when scaling circles using radius or diameter, we need to use the square root of the data values to get the circles to scale correctly, by area.)

The distortions of choropleth maps become a particular problem when displaying election results, where the significance of small geographical areas with large populations that have a major impact on the overall result gets downplayed, while sparsely populated large areas are overemphasized. Look at the “counties” and “size of lead” views in these maps of the 2012 Presidential election from The New York Times, and see which you think gives the clearest view of who won.

Choropleths: Choosing bins for your data

Another important consideration when making choropleth maps is how to set the “breaks” between the “bins” used to classify the data into different colors.

There is no simple answer to this question, as it really depends on the story you are telling. The map below reveals how setting different ranges for the bins changes the story told by the data. It shows the same data on GDP per capita in 2013 as in the previous choropleth mao, but this time I set the lower value for the top bin at $40,000, and then gave the other bins equal ranges:

(Source: Peter Aldhous, from World Bank data)

This might be useful for telling a story about how high per capita wealth is still concentrated into a small number of nations, but it does a fairly poor job of distinguishing between the per capita wealth of developing countries. And for poorer people, small differences in wealth make a big difference to living conditions.

So in the first version of the choropleth I set the boundaries so that roughly equal numbers of countries fell into each of the five bins. With these bins, Japan and most of Western Europe join the wealthiest bin, middle-income countries like Brazil, China, Mexico and Russia are grouped in another bin, and there are more fine-grained distinctions between the per capita wealth of different developing countries.

In making decisions like this, it can be helpful to look at the distribribution, or “shape” of the data, using a type of chart called a histogram. Here is a histogram for the 2013 GDP per capita data, showing a count of the countries for each increment of $2,500.

(Source: Peter Aldhous, from World Bank data)

Straight away we can see that just a tiny handful of countries had a GDP per capita of more than $50,000. Most countries are clustered at low values of GDP per capita, so to see differences between them, the breaks for the lower bins are going to have to be set fairly close together.

Most mapping software provides some automated options for dividing data into bins for a choropleth map. Here are those that you are most likely to encounter:

Cartograms

One solution to the main drawback of choropleth maps is to distort the areas plotted on the map to reflect aspects of the data, rather than geographical reality. These maps are called cartograms.

There are several algorithms for making cartograms which preserve the boundaries between geographical areas, which result in “organically” distorted maps. Here, for example, is a rendering of the 2012 Presidential Election results by county, distorted using the algorithm described in this scientific paper.

A good tool for making maps like this is Scapetoad. However, bear in mind that the impact of these maps derives from their disconcerting perspective. They can be useful to make your audience think about an issue in a new way, which was the thinking behind these maps of mine, comparing nations measured by GDP, and by other measures including the Happy Planet Index, which measures nations’ success in delivering long, contented lives for their citizens while minimizing the ecological damage that they cause.

(Source: Peter Aldhous, from World Bank and New Economics Foundation data)

Those cartograms retain common borders between areas, which constrains the accuracy with which areas can be resized according to values for a continuous variable. By relaxing this constraint, it is possible to resize areas more precisely, as seen in this example from Mike Bostock, a member of the graphics team at The New York Times.

However, bear in mind that it is hard to compare the areas of non-regular shapes, so either form of cartogram is not very useful if you want your audience to be able to “read” the data in a precise way.

It is also possible to make geometric cartograms, which use the area of shapes (generally circles or squares) to make a more abstract “map.” This graphic from The New York Times, published during the 2012 Presidential election campaign, took this approach.

Dot density maps: Seeing the big picture by showing all (or most) of the data

Sometimes patterns emerge from geographic data when we see the spatial distribution of every single occurrence of a phenomenon. This is the thinking behind dot density maps, like this visualization of the 2010 U.S. Census from the Weldon Cooper Center for Public Service at the University of Virginia, which includes a colored point for every single person:

The overall effect is rather like pointillist art. These maps work well when zoomed out, but are not so informative at high zoom levels.

A similar approach can work with aggregations of data, as in this project from The New York Times, which drew one dot for every 200 people, rather than one dot per person:

Making sense of many overlapping points: Heatmaps vs. hexagonal binning

While dot density maps can be useful on occasion, sometimes you may need to tell a story based on the distribution of points where they overlap, or sit directly on top of one another. This can present a misleading picture, as much of the data will be obscured.

Under such circumstances, other approaches are necessary. Heatmaps, for example, plot the density of points on a map as a gradient of colors, typically running from cool blues or greens to warm reds. Here, I used this approach to map violent events in Syria’s civil war from its start to the end of the first quarter of 2013, revealing “hotspots” of violence that were not so obvious from a map of thousands of overlapping points, seen below:

(Source: Peter Aldhous, from GDELT Project data)

While heatmaps are good for qualitatively identifying hotspots, they are less useful for communicating quantitative information. For this purpose, a better approach is to superimpose a hexagonal grid over the map, count the points in each cell, and use those counts to create a choropleth map, based on the grid:

(Source: Peter Aldhous, from GDELT Project data)

I used that approach on the same data to make this map of Syria’s conflict.

Think before you map: Is this the best representation of the data?

Whenever you come across data that can be put on a map, it’s very tempting to do this. However, always ask yourself: Is this the best way of telling my story? From the examples above, you will see that most maps encode data either using color, or through the area of circles or other symbols.

Now look again at the perceptual hierarchy of visual cues, and note that area and color intensity — the main options available when putting data onto maps — sit fairly low on the heirarchy.

This means that if you want to show differences in numerical values for some measure between U.S. states, for example, a map may be a poorer choice than a bar chart.

Consider these two representations of similar data on rates of overall gun death (a map from Rolling Stone) and gun homicides (a bar chart from Flowing Data) by U.S. state.

The bar chart clearly allows the more detailed comparison between rates for different states. However, the map still has value because it does show that the states with the highest gun death rates occur in particular geographic locations. In cases like this, consider using a map as only one part of your graphic, perhaps as a secondary element.

Using color effectively

Color falls low on the perceptual hierarchy of visual cues, but as we have already seen, it is often deployed to encode data values on maps. Poor choice of color schemes is a problem that bedevils many maps, so it is worth taking some time to consider how to use color to maximum effect.

It helps to think about colors in terms of the color wheel, which places colors that “harmonize” well together side by side, and arranges those that have strong visual contrast — blue and orange, for instance — at opposite sides of the circle:

(Source: Wikimedia Commons)

When encoding data with color, take care to fit the color scheme to your data, and the story you’re aiming to tell. As we have already noted, color is often used to encode the values of categorical data. Here you want to use “qualitative” color schemes, where the aim is to pick colors that will be maximally distinctive, as widely spread around the color wheel as possible.

When using color to encode numerical values, it usually makes sense to use increasing intensity, or saturation, of color to indicate larger values. These are called “sequential” color schemes.

In some circumstances, you may have data that has positive and negative values, or which highlights deviation from a central value. Here, you should use a “diverging” color scheme, which will usually have two colors reasonably well separated on the color wheel as its end points, and cycle through a neutral color in the middle:

Here are some examples of qualitative, sequential and diverging color schemes:

Choosing color schemes is a complex science and art, but there is no need to “roll your own” for every map you make. Mapping software usually includes suggested color palettes, but I often make use of the website from which the examples above were taken, called ColorBrewer. These color schemes have been rigorously tested to be maximally informative.

You will notice that the suggestions made by ColorBrewer can be displayed according to their values on three color “models”: HEX, RGB and CMYK. Here is a brief explanation of these and other common color models.

If you intend to roll your own color scheme, try experimenting with I want hue for qualitative color schemes, the Chroma.js Color Scale Helper for sequential schemes, and this color ramp generator, in combination with Colorizer or another online color picker, for diverging schemes.

You will also notice that ColorBrewer allows you to select color schemes that are colorblind safe. Surprisingly, many news organizations persist in using color schemes that exclude a substantial minority of their audience. Red and green lie on opposite sides of the color wheel, and also can be used to suggest “good” or “go,” versus “bad” or “stop.” But about 5% of men have red-green colorblindness, also known as deuteranopia.

Install Color Oracle to simulate how your maps will look to people with various forms of colorblindness.

Static vs. zoomable tiled maps

When designing a map-based graphic, one of the first things to decide is whether you want to display a static map view, or whether users should be able to pan and zoom the map in a dynamic way.

Web maps that can be panned and zoomed generally depend on a series of world maps of different zoom levels, which are each divided into square tiles. The tiles are loaded into the web browser as required as the user pans and zooms the map. This image demonstrates the principle:

(Source: Microsoft Developer Network)

Zoomable data-driven web maps are often displayed over basemaps from Google, OpenStreetMap, or another provider. Because these basemaps use a Mercator projection, that projection needs to be used for the data layers also.

Geographic data formats

CSV and other text files

Geographic data referring to points denoted by their latitude and longitude does not have to be saved in a specialized geodata format. Most mapping software can read data in plain text files, the most common format being CSV - for comma-separated values — in which fields in the data are separated by commas.

KML

KML, or Keyhole Markup Language, is the format used to display data on Google Earth and Google Maps. It is based on XML, a standard data format that is easily read by computers and is often used to move data around online. XML encodes data by placing it between nested “tags” that are similar to the tags used to encode elements of a web page in HTML.

In KML, tags can define a range of elements including points (such as the familiar placemarks used on Google Maps), lines, and the boundaries of geographical areas, known as “polygons.” The coordinates of these elements, their color and other aspects of their styling, and the information bubbles that may appear when the elements are clicked, can all be encoded in the KML.

Here, for example, is a simple KML file coding for an exaggeratedly tall representation of The Pentagon. Notice how the coordinates for the polygon give latitudes and longitudes that define the inner and outer boundaries of the building, and locate the “roof” at a height of 100 meters above ground level. <extrude>1</extrude> extends the shape to the ground:

<?xml version="1.0" encoding="UTF-8"?>
<kml xmlns="http://www.opengis.net/kml/2.2">
  <Placemark>
    <name>The Pentagon</name>
    <Polygon>
      <extrude>1</extrude>
      <altitudeMode>relativeToGround</altitudeMode>
      <outerBoundaryIs>
        <LinearRing>
          <coordinates>
            -77.05788457660967,38.87253259892824,100 
            -77.05465973756702,38.87291016281703,100 
            -77.05315536854791,38.87053267794386,100 
            -77.05552622493516,38.868757801256,100 
            -77.05844056290393,38.86996206506943,100 
            -77.05788457660967,38.87253259892824,100
          </coordinates>
        </LinearRing>
      </outerBoundaryIs>
      <innerBoundaryIs>
        <LinearRing>
          <coordinates>
            -77.05668055019126,38.87154239798456,100 
            -77.05542625960818,38.87167890344077,100 
            -77.05485125901024,38.87076535397792,100 
            -77.05577677433152,38.87008686581446,100 
            -77.05691162017543,38.87054446963351,100 
            -77.05668055019126,38.87154239798456,100
          </coordinates>
        </LinearRing>
      </innerBoundaryIs>
    </Polygon>
  </Placemark>
</kml>

This is what this file looks like when displayed in Google Earth:

(Source: Google Earth)

See Google’s tutorial and reference for a guide to the tags that can be used to code KML.

KML can also be compressed into KMZ files. To create a KMZ file from KML, open the file in Google Earth, right-click on the file in the Places panel, select Save Place As, and then select KMZ under format.

KML has been adopted as a standard for geographic data, and so can be used by a wide range of mapping applications, including Geographic Information Systems (GIS) software.

GeoJSON

GeoJSON is a variant of JSON, or JavaScript Object Notation, a data format commonly used by “application programming interfaces,” or APIS, which can be queried online to request specific data. GeoJSON is also commonly used to store the data for online maps.

JSON treats data as a series of “objects,” which begin and end with curly brackets. Each object in turn contains a series of name-value pairs. There is a colon between the name and value in each pair, and the pairs are separated by commas.

GeoJSON obeys this structure, but has a number of specific elements: Each Feature has properties, which can be any data related to the feature, geometry, which includes its type (point, line, polygon and so on), and latitude and longitude coordinates. Features can be grouped into a FeatureCollection. Here, for example, are ten addresses in San Francisco, encoded as GeoJSON:

{
"type": "FeatureCollection",
"crs": { "type": "name", "properties": { "name": "urn:ogc:def:crs:OGC:1.3:CRS84" } },

"features": [
{ "type": "Feature", "properties": { "address": "1800 25th St, San Francisco, CA, 94107"}, "geometry": { "type": "Point", "coordinates": [ -122.397484, 37.753067 ] } },
{ "type": "Feature", "properties": { "address": "302 Silver Ave, San Francisco, CA, 94112"}, "geometry": { "type": "Point", "coordinates": [ -122.430573, 37.727722 ] } },
{ "type": "Feature", "properties": { "address": "425 7th St, San Francisco, CA, 94103"}, "geometry": { "type": "Point", "coordinates": [ -122.404366, 37.775398 ] } },
{ "type": "Feature", "properties": { "address": "2001 Chestnut St, San Francisco, CA, 94123"}, "geometry": { "type": "Point", "coordinates": [ -122.436508, 37.800575 ] } },
{ "type": "Feature", "properties": { "address": "952 Sutter St, San Francisco, CA, 94109"}, "geometry": { "type": "Point", "coordinates": [ -122.416161, 37.788548 ] } },
{ "type": "Feature", "properties": { "address": "105 Palm Ave, San Francisco, CA, 94118"}, "geometry": { "type": "Point", "coordinates": [ -122.458206, 37.783619 ] } },
{ "type": "Feature", "properties": { "address": "1111 California St, San Francisco, CA, 94108"}, "geometry": { "type": "Point", "coordinates": [ -122.412956, 37.791183 ] } },
{ "type": "Feature", "properties": { "address": "1501 Larkin St, San Francisco, CA, 94109"}, "geometry": { "type": "Point", "coordinates": [ -122.419556, 37.791859 ] } },
{ "type": "Feature", "properties": { "address": "4508 Balboa St, San Francisco, CA, 94121"}, "geometry": { "type": "Point", "coordinates": [ -122.507271, 37.77549 ] } },
{ "type": "Feature", "properties": { "address": "101 Turk St, San Francisco, CA, 94102"}, "geometry": { "type": "Point", "coordinates": [ -122.411064, 37.78289 ] } }
]
}

See the full GeoJSON specification for more details.

TopoJSON is an extension of GeoJSON that is more compact for encoding polygons, because they are described by line segments, rather than their entire boundaries. This means that the boundary between California and Nevada, for instance, is represented only once, rather than twice — once for each state. This keeps file sizes small, which can be advantageous when data must be loaded and rendered in a web browser.

Shapefile

This is a geodata format developed by ESRI, manufacturer of ArcGIS, the leading commercial GIS application. Shapefiles can represent elements including points, lines and polygons, and can also include information on map projection and datums.

Shapefiles are usually made available for download as zipped folders, and actually consist of a series of files. At a minimum, a shapefile must contain three component files, with the same root name and the following extensions:

There are several optional file types that may also be included, including a .prj file, which defines the map projection and datum to be used when loading the shapefile into GIS software. Refer to ESRI’s technical specification and the informative Wikipedia entry for more details.

Many government agencies, such as the U.S. Census Bureau, provide data for mapping as shapefiles. You can also download shapefiles from repositories such as Natural Earth.

Converting between geodata formats

We will later learn how to use QGIS to convert between the main geodata formats. You can also use the Mapshaper web app to convert between shapefiles, GeoJSON and TopoJSON. The ShapeEscape web app will also convert zipped shapefiles to GeoJSON and TopoJSON, or upload them to Google Fusion Tables, from where you can download KML.

Starting to work with data: APIs, geocoding and distributions

For the remainder of this session we will start to work with data that we will put onto maps later in the workshop.

The data we will use

Download the data from this session from here, unzip the folder and place it on your desktop. It contains two subfolders, with the following files:

GDP
Geocoding

The geocoding files can also be downloaded from my GitHub account — click the Download ZIP button at right.

Use an API to obtain geodata

Increasingly, organizations that publish data are making it avilable over the web using APIs. These can be queried by constructing a URL in a specific format to return specified data. This allows websites and apps to call in specific chunks of data as required, and work with it “on the fly.” APIs can be particularly useful when making online maps that you want to update automatically when new data becomes available.

To see how this works, go to the U.S. Geological Survey’s Earthquake Archive Search & URL Builder, where we will search for all earthquakes with a magnitude of 5 or greater that occured witin 6,000 kilometres of the geographic center of the contiguous United States, which this site tells us lies at a latitude of 39.828175 degrees and a longitude of -98.5795 degrees. We will initially ask for the data as GeoJSON. Enter 1900-01-01T00:00:00 under Start for Date & Time boxes so that we obtain all recorded earthquakes from the beginning of 1900 onward. The search form should look like this:

(Source: U.S. Geological Survey)

You should recieve a quantity of data at the following url:

http://comcat.cr.usgs.gov/fdsnws/event/1/query?starttime=1900-01-01T00:00:00&latitude=39.828175&longitude=-98.5795&maxradiuskm=6000&minmagnitude=5&format=geojson&orderby=time

See what happens if you append -asc to the end of that url: This should sort the the earthquakes from oldest to newest, rather than the default of newest to oldest. Here is the full documentation for querying the earthquakes API by manipulating these URLs,

Now remove the -asc and replace geojson in the URL with csv. The data should now download in CSV format.

We will use data obtained using the USGS earthquakes API in later sessions in this workshop.

Geocode to latitude and longitude coordinates from addresses

Often when starting a mapping project, you may need to convert a series of addresses into latitudes and longitudes so they can be placed on your map. This is called geocoding.

There are several geocoding APIs, which can be accessed in various ways. The number of requests allowed per day and the terms of use vary from service to service: Google’s free service, for instance, allows each user to geocode 2,500 addresses per day, and specifies that the resulting coordinates may only be used to make a Google Map.

Because of this restriction, we will instead use the services offered by Microsoft’s Bing Maps, and MapQuest (which is based on OpenStreetMap’s Nominatim service), to geocode our sample of San Francisco addresses.

To access these APIs and process the data returned, we will use Open Refine (formerly Google Refine). It can streamline many data processing and cleaning tasks, and will reward efforts to explore its wide range of its functions — see the further reading/viewing, below.

When you launch Open Refine, it will open in your web browser. However, any data you load into the program will remain on your computer — it does not get posted online.

The opening screen should look like this:

Click the Browse button and navigate to the file sf_test_addresses_short.tsv. (Don’t use the full version of the file for this initial exercise, as it will take a long time to process!)

Click Next>>, and check that data looks correct:

Open Refine should recognize that the data is in a TSV file, but if not you can use the panel at bottom to specify the correct file type and format for the data

When you are statisfied that the data has been read correctly, click the Create Project >> button at top right. The screen should now look like this:

Here is how to geocode addresses from Open Refine using the Bing API:

You will need a Bing Maps API key. To obtain one, follow the steps here. If you don’t already have a Microsoft Account, you will first need to create one.

In your Open Refine project, click the address column, click on the small downward-pointing triangle and select Edit column>Add column by fetching URLs.... You will see the following dialog box:

Call the new column bing_json and enter the following following expression:

"http://dev.virtualearth.net/REST/v1/Locations?q=" + escape(value, "url") + "&key=BingMapsKey"

Note that you will have to enter your own Bing API key in place of BingMapsKey. Also, set the Throttle delay to 500 milliseconds for faster processing. This expression constructs a URL that will query the Bing geocoding API and return data for each address in JSON format.

From the bing_json column, select Edit column>Add column based on this column..., call the column bing_lat_lon and use this expression to extract the latitude and longitude from the JSON returned by the API:

with(value.parseJson().resourceSets[0].resources[0].point.coordinates, pair, pair[0] +", " + pair[1])

Split the bing_lat_lon column into to two columns by selecting Edit column>Split into several columns, then rename these columns bing_latitude and bing_longitude by selecting Edit column>Rename this column.

From the bing_json column, select Edit column>Add column based on this column..., call the column bing_confidence and use this expression to extract the Bing API’s confidence in the accuracy of its geocoding:

with(value.parseJson().resourceSets[0].resources[0].confidence, v, v)

From the bing_json column, select Edit column>Add column based on this column..., call the column bing_type and use this expression to extract the type of place that the Bing API has geocoded:

with(value.parseJson().resourceSets[0].resources[0].entityType, v, v)

For a full address, this should return Address when the geocoding has been successful.

Finally, delete the bing_json column by selecting Edit column>Remove column.

The data should now look like this:

One particularly nice attribute of Open Refine is that you can save a script that will allow you to repeat the same processing on future iterations of the same data. To access this, select the Undo/Redo tab at top left and click Extract. The right-hand panel contains data in JSON format that describes the operations we just ran on the data. Copy this, paste into a blank text file and save.

While I wanted you to see how geocoding with Open Refine depends on interactions with APIs, there’s no need to perform this process manually each time you need to geocode some data. Instead, you can use the file refine-geocoder.json, which I extracted from Open Refine as described above. It will geocode a simple list of addresses using both the Bing and MapQuest APIs.

For the MapQuest results, the mapquest_class column provides information on the accuracy of geocoding: place, amenity or shop indicate geocoding to a precise address; highway indicates geocoding to a street only. The mapquest_type column provides further information about the address or street .

Open the refine-geocoder.json file in a text editor (I recommend TextWrangler if you are working on a Mac, Notepad++ if you are on a Windows machine), and perform a find-and-replace, replacing BingMapsKey with your own Bing maps key. Then copy all the text in the file, and save it for future use.

Start a new Open Refine project using the file sf_test_addresses.tsv, containing 100 addresses. When the data has imported, select the Undo/Redo tab, and click Apply. Paste in the text from your edited refine-geocoder.json file and then click Perform Operations. Open Refine will then geocode the addresses — a process that will take some time.

The Bing and MapQuest services can also be accessed through the GPS Visualizer geocoder. To geocode addresses in bulk from this site using MapQuest, you will need to obtain a MapQuest AppKey, following these instructions.

Whichever service you use to geocode addresses, provide appropriate attribution. MapQuest’s terms and conditions require that you include this acknowledgement on any website or app using data geocoded through its service:

<p>Geocoding Courtesy of <a href="http://www.mapquest.com/" target="_blank">MapQuest</a> <img src="http://developer.mapquest.com/content/osm/mq_logo.png"></p>

Data should also be sourced to OpenStreetMap, see here for instructions on how to credit appropriately.

Here is an HTML acknowledgment to Bing in the same style as above:

<p>Geocoding Courtesy of <a href="http://www.microsoft.com/maps/product/terms.html" target="_blank">Bing</a> <img src="http://www.microsoft.com/maps/images/branding/Bing%20logo%20gray_50px-19px.png"></p>

Be aware that different geocoders will give slightly different results. In my experience, MapQuest tends to locate addresses to sidewalks or building fronts, while Bing tends to locate to the middle of the building concerned. Bing’s failure rate also appears to be lower. You may need to manually record the coordinates of addresses that fail, or which do not geocode to a precise address. In these cases, try searching for the address on Bing Maps or Google Maps. For the latter, note the latitude and longitude for the placemarker than appears, shown here after the @ symbol:

https://www.google.com/maps/place/1875+Cesar+Chavez+St,+San+Francisco,+CA+94107/@37.7497825,-122.395751,17z/data=!3m1!4b1!4m2!3m1!1s0x808f7fae0a545527:0x564005c073e75262

Other options for geocoding include Texas A&M University’s GeoServices, which will geocode from an uploaded text file, emailing you when the results are ready for download. First sign up for a free account, then upload your data.

Explore distributions of data

As we noted earlier, exploring the distribution of data may be useful when deciding how to divide it into bins if making a choropleth map.

For this task we will use this web app, written by statistician and programmer Jeroen Ooms. It provides a point-and-click interface to ggplot2, a charting library for the R programming language, and makes it easy to draw statistical graphics.

In your browser, navigate to the app, which looks like this:

From the top menu, select Open Data>Upload File (note that there is also on option to open from a Google Spreadsheet), then click Browse to navigate to the file gdp_pc_2013.csv and Open. Check that the data seems to be importing properly, with a header row and the fields identified correctly. (You can try adjusting the import options if there are any problems.)

Click Import and open the folders in the Data Panel at top right to see that the country names and three-letter codes (iso_a3) appear under Factor and the values for GDP per capita under Numeric:

First we need to tell the app what to plot on the X and Y axis, respectively. Right-click anywhere in the main panel and select Map x(required)>gdp_pc. We are not going to plot another variable from the data on the Y axis; instead we just want a count of the countries in each salary in each increment of GDP per capita, so select Map y(required)>..count...

If at this point you click the Draw Plot button at bottom right, you will see a blank grid, because we haven’t yet told the app what type of chart to draw. Right-click again in the chart area, and select Add Layer>Univariate Geoms>histogram (univariate because we only have one variable, aggregated by a count). Click Draw plot and a chart should appear:

You may notice that the columns are wider than in the version of this chart I showed earlier. Right-click on histogram in the Layers Panel at top left, select binwidth>set, type 2500 into the box and click set value. Now click Draw plot again to see the following plot:

To save your plot click on Export PDF from the options at top left and click on the hyperlink at the next page.

Further reading/viewing

Mark Monmonier: How to Lie With Maps
This popular exploration of how all maps distort reality, and how some can seriously deceive, provides a good overview of cartographic principles.

Open Refine demo videos

Open Refine Wiki

Open Refine Documentation

Open Refine Recipes

ggplot2 web app demo video